
What is the z-score of a measured value of 0.0034, given µ = 0.0041 and σ = 0.0008?.What is the z-score of the weight of a cow that tips the scales at 825 lbs, if the mean weight for cows of her type is 1150 lbs, with a standard deviation of 77 lbs?.What is the z-score of a 5-scoop ice cream cone if the mean number of scoops is 3, with a standard deviation of 1 scoop?.What is the z-score of the price of a pair of skis that cost $247, if the mean ski price is $279, with a standard deviation of $16?.
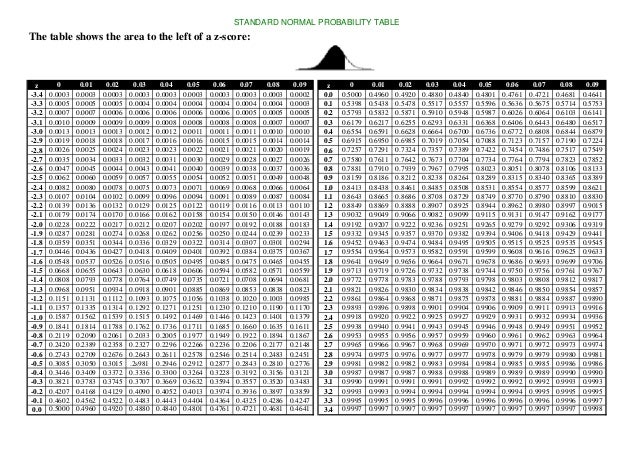
#Z SCORE TABLE HOW TO#
In the next lesson, we will learn how to associate the z-score of a value with the probability that the value will occur. In this lesson, we will practice calculating the z-score for various values. You calculate the z-score by first calculating the difference between your value and the mean, and then dividing that amount by the standard deviation of the set. While the Empirical Rule allows you to associate the first three standard deviations with the percentage of data that each SD includes, the z-score allows you to state (as accurately as you like), just how many SDs a given value is above or below the mean.Ĭonceptually, the z-score calculation is just what you might expect, given that you are calculating the number of SDs between a value and the mean. You can think of a z-score as the number of standard deviations there are between a given value and the mean of the set. Z-scores are related to the Empirical Rule from the standpoint of being a method of evaluating how extreme a particular value is in a given set. It is worth noting, particularly for US students, that the instructor uses the notation x bar (a bar over the x) rather than µ for mean, and pronounces z as “zed.”
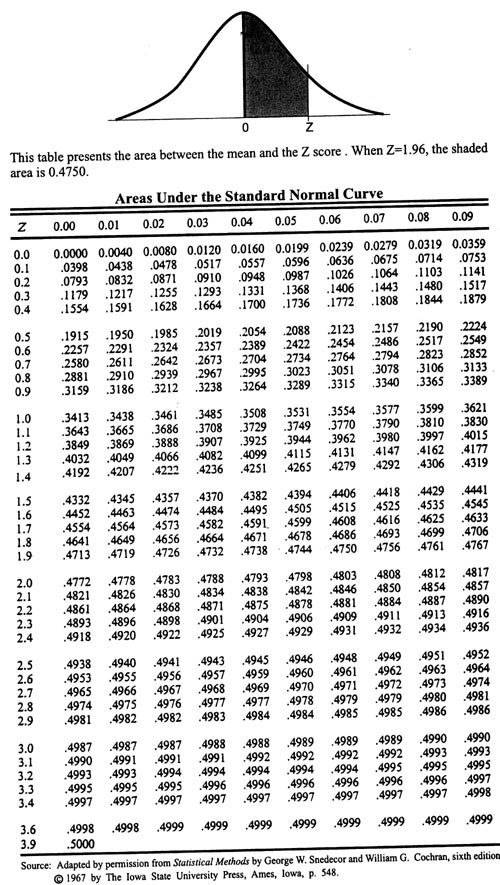
The British video below is very clear and easy to follow.


 0 kommentar(er)
0 kommentar(er)
